Implementation and evaluation of data-compression algorithms for irregular-grid iterative methods on the PEZY-SC processor

  • Naoki Yoshifuji (Fixstars)
  • Ryo Sakamoto (Fixstars, present: PEZY Computing)
  • Keigo Nitadori (RIKEN AICS)
  • Jun Makino (Department of Planetology, Kobe University)

IA3 2016 Sixth Workshop on Irregular Applications: Architectures and Algorithms (SC16 Workshop) @ Salt Lake City, UT

Talk Summary

  • HPCG was implemented on PEZY-SC on ZettaScaler system
  • Single-chip performance of SpMV is 11.6 GFLOPS, which is 93% of the theretical limit determined by the memory bandwidth
  • Simple and fast matrix compression were applied to SpMV and tested
  • Data+Index table-based compression improved performance by a factor of 2.8

Data compression can be very powerful way to improve performance of unstructured grid calculation

Introduction

Contents

  1. Introduction
  2. PEZY-SC and ZettaScaler
  3. HPCG on PEZY
  4. SpMV with compression
  5. Conclusion

To solve linear equations

Many real problems (e.g. FEM or other CAE problems) requires to solve large linear equations:

\[A \boldsymbol{x} = \boldsymbol{b}\]

\(A\) is large sparse and irregular matrix in most cases of real problems

Iterative methods are suited

Multiplication of sparse matrix and vector (SpMV) is the most time-consuming process

SpMV is slow on modern HPC systems

Example: Top 3 of June 2016 HPCG results
RankComputerRpeakHPCGHPCG/Rpeak
1MilkyWay-254.90.581.1%
2K computer11.30.554.9%
3Sunway TaihuLight125.40.370.3%

Modern computer's memory bandwidth is too small against (arithmetic) instruction throughput for SpMV

Our propposal

A simple data compression and decompression
for sparse matrix
↓
Reduce memory access
↓
Improve performance

PEZY-SC and ZettaScaler

Contents

  1. Introduction
  2. PEZY-SC and ZettaScaler
  3. HPCG on PEZY
  4. SpMV with compression
  5. Conclusion

Why PEZY-SC?

  • MIMD processor
    →easy implementation
  • Byte per Flop is very small
    →easy to check compression efficiency

HPCG on PEZY

Contents

  1. Introduction
  2. PEZY-SC and ZettaScaler
  3. HPCG on PEZY
  4. SpMV with compression
  5. Conclusion

Why HPCG?

  • A standard benchmark for iterative method (MGCG)
  • Its model is close to real problem (3D diffusion eq.)

Result of HPCG on PEZY

Achieved 168.06 GFLOPS with 8 nodes (32 PEZY-SCs)

Fraction of time consuming

SpMV analysis

93% of the theoretical limit

Achieved
11.6 GFLOPS
Theoretical by memory bandwidth
12.5 GFLOPS

SpMV with compression

Contents

  1. Introduction
  2. PEZY-SC and ZettaScaler
  3. HPCG on PEZY
  4. SpMV with compression
  5. Conclusion

Matrix in HPCG

Illustration of the matrix in HPCG
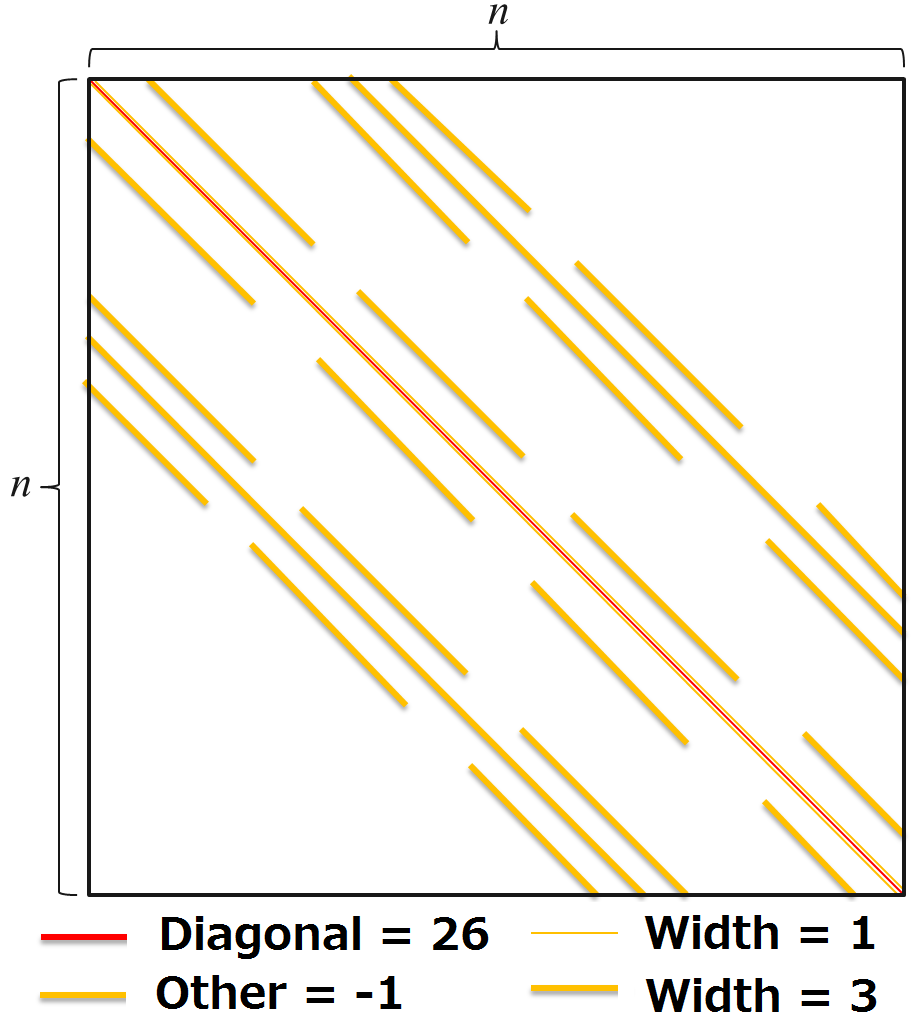
  • 2 same values
  • Several same patterns for non-diagonal position

Matrix in real application

Same coefficients
If the physical characteristics of the material is uniform
Same relative index pattern
If we can use effectively regular grids for the bulk of the material

Table-based sparse matrix compression

Data table compression
extract same value of matrix elements
Index table compression
extract same pattern of column number

SpMV result on HPCG matrix

CompressionAchieved GFLOPSTheoretical GFLOPSratio (achieved/theretical)
None11.612.5x1.0 / x1.0
Data table15.934.8x1.4 / x2.8
Data+Index table32.4326.0x2.8 / x26.1

NOTE: theoretical estimate ignores input vector random access

Conclusion

Contents

  1. Introduction
  2. PEZY-SC and ZettaScaler
  3. HPCG on PEZY
  4. SpMV with compression
  5. Conclusion

Conclusion

  • HPCG was implemented on PEZY-SC on ZettaScaler system
  • Single-chip performance of SpMV is 11.6 GFLOPS, which is 93% of the theretical limit determined by the memory bandwidth
  • Simple and fast matrix compression were applied to SpMV and tested
  • Data+Index table-based compression improved performance by a factor of 2.8

Compression technique will improve solver for linear equations in CAE application and others on the current and future HPC system!

Acknowledgment

  • The authors would like to thank people in PEZY Computing/ExaScaler for their invaluable help in solving many problems we encountered while porting and tuning HPCG.
  • Part of the research covered in this paper research was funded by MEXT’s program for the Development and Improvement for the Next Generation Ultra High-Speed Computer System, under its Subsidies for Operating the Specific Advanced Large Research Facilities.
return 0;